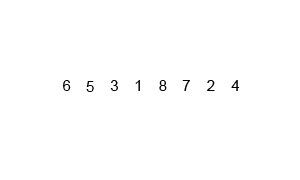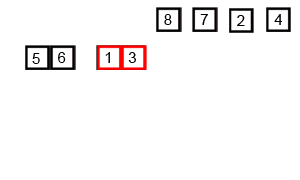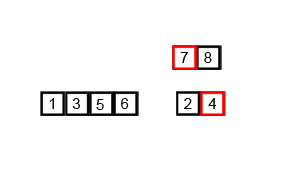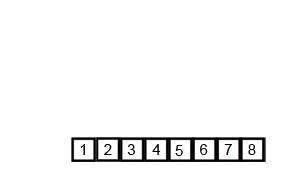병합 정렬 [Merge Sort]

참고

---

Link

daleseo.com/sort-merge/

gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

---

Merge Sort

---

하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법임.

합병 정렬은 다음의 단계들로 이루어짐.

1. 분할(Divide)
   • 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
2. 정복(Conquer)
   • 부분 배열을 정렬, 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용함.
3. 결합(Combine)
   • 정렬된 부분 배열들을 하나의 배열에 합병함.

과정 요약

1. 리스트 길이가 0 또는 1이면 이미 정렬된 것으로 봄.

2. 그렇지 않은 경우에는 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눔.

3. 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬함.

4. 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병함.

시간복잡도는 O(nlogn), 단점은 정렬된 데이터 배열을 담을 새로운 배열이 필요하여 추가적인 메모리가 사용된다는 점임.

---

Code

---

def merge(larr,rarr) :
    i=j=0 
    temp=[]
    while i < len(larr) and j < len(rarr) :
        if larr[i] <= rarr[j] :
            temp.append(larr[i])
            i+=1
        else :
            temp.append(rarr[j])
            j+=1
    temp+=larr[i:]
    temp+=rarr[j:]
    return temp

def merge_sort(arr) :
    if len(arr) < 2 :
        return arr
    
    mid=len(arr)//2
    larr=merge_sort(arr[:mid])
    rarr=merge_sort(arr[mid:])
    
    return merge(larr,rarr)

# 가져온 코드
def merge_sort(arr):
    if len(arr) < 2:
        return arr

    mid = len(arr) // 2
    low_arr = merge_sort(arr[:mid])
    high_arr = merge_sort(arr[mid:])

    merged_arr = []
    l = h = 0
    while l < len(low_arr) and h < len(high_arr):
        if low_arr[l] < high_arr[h]:
            merged_arr.append(low_arr[l])
            l += 1
        else:
            merged_arr.append(high_arr[h])
            h += 1
    merged_arr += low_arr[l:]
    merged_arr += high_arr[h:]
    return merged_arr

---